Research
CBO Working Papers
How CBO Projects Inflation (2024)
Dissertation Chapters
Chapter 3: Bounded Rationality in Macroeconomic: A Continuous-Time Approach
We reconsider optimal decision making in a continuous-time framework using adaptive learning, specifically shadow-price learning; we explore these dynamics in a real business cycle framework. The agent in our shadow-price learning model takes in information and updates their forecasts of future states and their decisions regarding choice variables. In our setting, the agent makes decisions at high frequencies, which alters the volatility of the agent’s parameter estimates and leads to smoother real-time convergence to the rational expectations equilibrium. We attribute the less volatile convergence to the agent’s ability to alter their forecasts more often as new information becomes available. We also investigate alternative sampling methods where the data generating process is a higher frequency than the agent’s observations; these sampling methods yield similar results to the case where the agent takes in all data points and are less computationally burdensome.
Chapter 2: Boundedly Rational Decision Making in Continuous-Time
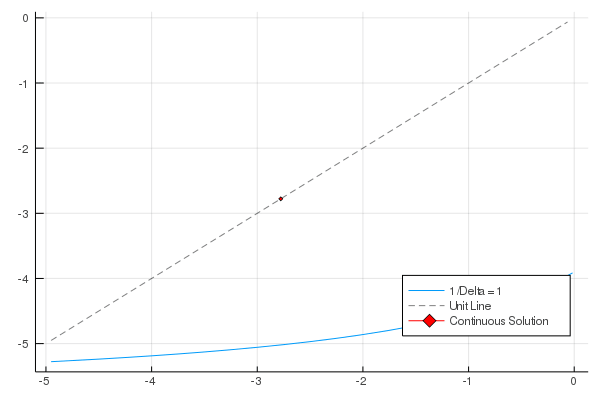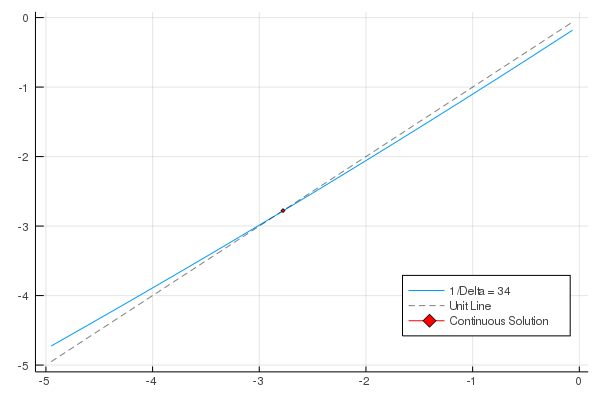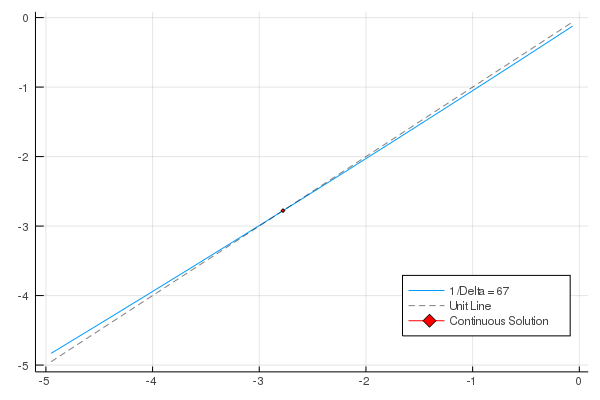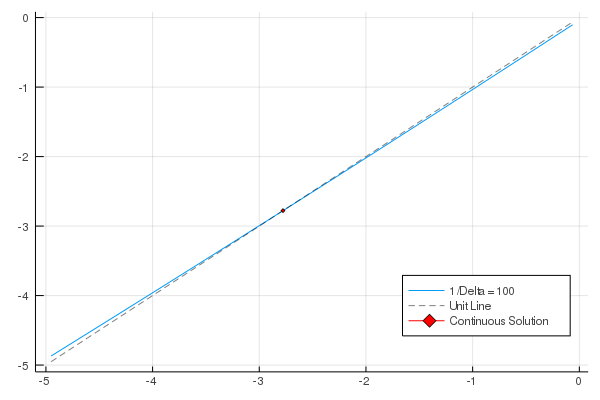 Continuous-time macroeconomic literature has grown remarkably in recent
years. As work on continuous-time models becomes, more prevalent macroeconomists need to adapt essential discrete-time methods to continuous-time.
This paper modifies adaptive learning techniques to continuous-time. One approach to accomplish this task is shadow-price learning (SP-learning), a framework in which agents forecast their expected shadow prices. To use this framework efficiently, we first need a tractable continuous-time linear-quadratic (LQ)
environment. While discrete-time LQ problems are common in the literature,
there is very little work on continuous-time LQ problems. Thus, our contributions are two-fold. We build a continuous-time LQ framework for solving
Hamilton-Jacobi-Bellman (HJB) equations using iterative methods and implement adaptive learning techniques in this new setting.
Continuous-time macroeconomic literature has grown remarkably in recent
years. As work on continuous-time models becomes, more prevalent macroeconomists need to adapt essential discrete-time methods to continuous-time.
This paper modifies adaptive learning techniques to continuous-time. One approach to accomplish this task is shadow-price learning (SP-learning), a framework in which agents forecast their expected shadow prices. To use this framework efficiently, we first need a tractable continuous-time linear-quadratic (LQ)
environment. While discrete-time LQ problems are common in the literature,
there is very little work on continuous-time LQ problems. Thus, our contributions are two-fold. We build a continuous-time LQ framework for solving
Hamilton-Jacobi-Bellman (HJB) equations using iterative methods and implement adaptive learning techniques in this new setting.
Chapter 1 : Adaptive Learning in a Continuous-Time Setting: Representative Agent Exercises (Third-Year Paper)
We accomplish two distinct, but closely connected, tasks in this paper. First, We look to create a connection between discrete and continuous-time models. This is done by recasting traditional discrete Ramsey models so they are dependent on the increment of time, Δ, and then taking the limit of these models as the size of this increment goes to zero. The resulting models are equivalent to continuous-time Ramsey models. Second, We examine these models in a basic adaptive learning framework. We accomplish this by applying exogenous updating rules to models with a specified stochastic process. After seeing that the misspecified models converge, We then implement a real-time updating rule where agents update their parameter estimates—for a stochastic process—after observing output of the process.
For more information and code from this project visit my repo.